（本小题满分12分）设函数
的图象上两点P1(x1，y1)、P2(x2，y2)，若
，且点P的横坐标为
．
(1)，求证：P点的纵坐标为定值，并求出这个定值；
(2)，求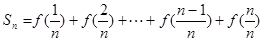
(3)，记Tn为数列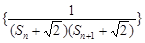
的前n项和，若
对一切n∈N*都成立，试求a的取值范围。
相关试题
中,
⊥底面
,四边形
⊥
,
,
,
.
⊥平面
；
的距离；
中，角
所对的边分别为
，且
．
的值；（2）若
，求
的取值范围．
中，
，其前
项和为
，等比数列
的各项均为正数，
，公比为
，且
，
.
与
；（2）设数列
满足
，求
的前
.
的最小值及取最小值时
的值。
，求
的取值范围。
的前
项和
，数列
满足
．
，数列
的前
，求满足
的推荐套卷
（本小题满分12分）设函数的图象上两点P1(x1，y1)、P2(x2，y2)，若，且点P的横坐标为．
(1)，求证：P点的纵坐标为定值，并求出这个定值；
(2)，求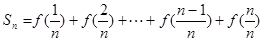
(3)，记Tn为数列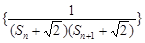的前n项和，若对一切n∈N*都成立，试求a的取值范围。
粤公网安备 44130202000953号