(本小题满分11分)对于定义域为D的函数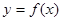
，如果存在区间
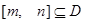，同时满足：
①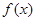
在
内是单调函数；
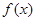②当定义域是时，的值域也是．
则称是该函数的“和谐区间”．
（1）证明：
是函数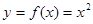
的一个“和谐区间”．
（2）求证：函数
不存在“和谐区间”．
（3）已知函数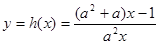
（
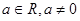）有“和谐区间”，当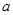
变化时，求出
的最大值．
在
时有最大值1，
，并且
时，
的取值范围为
. 试求m，n的值.
，
是互不相同的正整数，
.
，
为给定的整数，
. 对任意
，作
，集合
，求
型五方连块？
，其中
，且
．求
的最大值和最小值．推荐套卷
(本小题满分11分)对于定义域为D的函数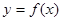，如果存在区间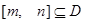，同时满足：
①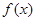在内是单调函数；
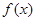②当定义域是时，的值域也是．
则称是该函数的“和谐区间”．
（1）证明：是函数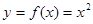的一个“和谐区间”．
（2）求证：函数不存在“和谐区间”．
（3）已知函数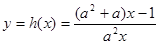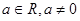（）有“和谐区间”，当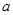变化时，求出的最大值．
粤公网安备 44130202000953号