如图,点D在反比例函数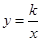 ( k>0)上,点C在
( k>0)上,点C在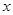 轴的正半轴上且坐标为(4,O),△ODC是以CO为斜边的等腰直角三角形.
轴的正半轴上且坐标为(4,O),△ODC是以CO为斜边的等腰直角三角形.
⑴ 求反比例函数的解析式;
⑵ 点B为横坐标为1的反比例函数图象上的一点,BA、BE分别垂直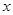 轴和
轴和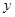 轴,垂足分别为点A和点E,连结OB,将四边形OABE沿OB折叠,使A点落在点A′处,A′B与
轴,垂足分别为点A和点E,连结OB,将四边形OABE沿OB折叠,使A点落在点A′处,A′B与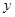 轴交于
轴交于
点F.求直线BA′的解析式.
相关知识点
推荐套卷
如图,点D在反比例函数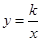 ( k>0)上,点C在
( k>0)上,点C在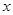 轴的正半轴上且坐标为(4,O),△ODC是以CO为斜边的等腰直角三角形.
轴的正半轴上且坐标为(4,O),△ODC是以CO为斜边的等腰直角三角形.
⑴ 求反比例函数的解析式;
⑵ 点B为横坐标为1的反比例函数图象上的一点,BA、BE分别垂直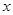 轴和
轴和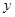 轴,垂足分别为点A和点E,连结OB,将四边形OABE沿OB折叠,使A点落在点A′处,A′B与
轴,垂足分别为点A和点E,连结OB,将四边形OABE沿OB折叠,使A点落在点A′处,A′B与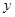 轴交于
轴交于
点F.求直线BA′的解析式.