如图①,△ABC与△DEF为等腰直角三角形,CB与EF重合,AC=DE=8,∠ACB=∠DEF=90°固定△ABC,将△DEF绕点C顺时针旋转,当边FE与边CA重合时,旋转终止。设FE、FD(或它的延长线)分别交AB(或它的延长线)于点P、Q,如图②
(1)问:始终与△CPB相似的三角形(不添加其他辅助线)有① 及②
(2)设BP=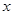 ,AQ=
,AQ=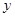 ,求
,求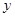 关于
关于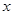 的函数关系式;
的函数关系式;
(3)问:当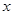 为何值时,△CPQ是等腰三角形?
为何值时,△CPQ是等腰三角形?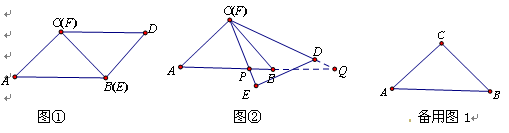
相关知识点
推荐套卷
 )÷
)÷
 ÷
÷ ,其中a=﹣
,其中a=﹣ ,b=1.
,b=1.
 (k>0)的图象与直线l交于C、D两点,连接OC、OD.
(k>0)的图象与直线l交于C、D两点,连接OC、OD.


 粤公网安备 44130202000953号
粤公网安备 44130202000953号