某生态示范园要对1号、2号、3号、4号四个新品种共500株果树幼苗进行成活实验,从中选出成活率高的品种进行推广.通过实验得知:3号果树幼苗成活率为89.6%,把实验数据绘制成下列两幅统计图(部分信息未给出).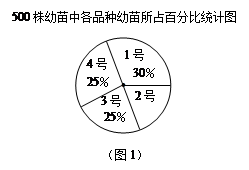

(1)实验所用的2号果树幼苗的数量是_______株;
(2)求出3号果树幼苗的成活数,并把图2的统计图补充完整;
(3)你认为应选哪一种果树幼苗进行推广?请通过计算说明理由.
相关知识点
推荐套卷
某生态示范园要对1号、2号、3号、4号四个新品种共500株果树幼苗进行成活实验,从中选出成活率高的品种进行推广.通过实验得知:3号果树幼苗成活率为89.6%,把实验数据绘制成下列两幅统计图(部分信息未给出).

(1)实验所用的2号果树幼苗的数量是_______株;
(2)求出3号果树幼苗的成活数,并把图2的统计图补充完整;
(3)你认为应选哪一种果树幼苗进行推广?请通过计算说明理由.