某体育用品商店试销一款成本为50元的排球，规定试销期间单价不低于成本价，且获利不得高于40%．经试销发现，销售量y（个）与销售单价x（元）之间满足如图所示的一次函数关系。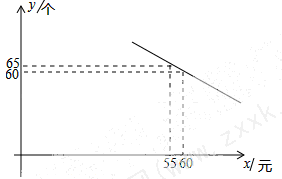
（1）试确定y与x之间的函数关系式；
（2）若该体育用品商店试销的这款排球所获得的利润Q元，试写出利润Q（元）与销售单价x（元）之间的函数关系式；当试销单价定为多少元时，该商店可获最大利润？最大利润是多少元？
（3）若该商店试销这款排球所获得的利润不低于600元，请确定销售单价x的取值范围．
相关试题
（本小题10分）如图，两座建筑物的水平距离
为30m，从
点测得
点的俯角
为35°，测得
点的俯角
为43°，求这两座建筑物的高度（结果保留小数点后1 位，参考数据
，
，
，
，
，
）．
（本小题10分）已知AB，BC，CD分别与⊙
相切于E，F，G三点，且AB∥CD，连接OB，OC．
（1）如图①，求∠BOC的度数；
（2）如图②，延长CO交⊙O于点M，过点M做MN∥OB交CD于点N，当OB=6，OC=8时，求⊙的半径及MN的长．
+bx+c过点（0，0），（1，3），求抛物线的解析式，并求出抛物线的顶点坐标．
；
的根的情况．相关知识点
推荐套卷
粤公网安备 44130202000953号