如图，要测量池塘A、B两点间的距离，可以在AB的垂线BF上取两点C、D，使CD=BC，再过D点作出BF的垂线DG，并在DG上找一点E，使点A、C、E在一条直线上，这时，测量DE的长就是AB的长，为什么？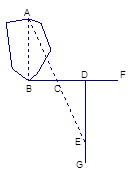
中，
是
上的一点，
，在
上是否存在一点
，使
三点组成的三角形与
的长；如果不存在，请说明理由．
分别为边
的三等分点（即：
），若
，求
的大小．
为
的中点，求
的周长．
若
cm，
cm，试求
的长．
，若
cm，求
的长．
相关知识点
推荐套卷
如图，要测量池塘A、B两点间的距离，可以在AB的垂线BF上取两点C、D，使CD=BC，再过D点作出BF的垂线DG，并在DG上找一点E，使点A、C、E在一条直线上，这时，测量DE的长就是AB的长，为什么？
粤公网安备 44130202000953号