探索归纳:
(1)如图1,已知△ABC为直角三角形,∠A=90°,若沿图中虚线剪去∠A,则∠1+∠2等于 ( )
| A.90° | B.135° | C.270° | D.315° |
(2)如图2,已知△ABC中,∠A=40°,剪去∠A后成四边形,则∠1+∠2=_______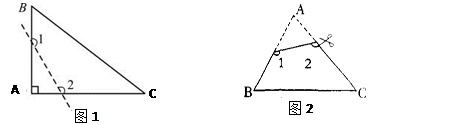
(3)如图2,根据(1)与(2)的求解过程,请你归纳猜想∠1+∠2与∠A的关系是________________
(4)如图3,若没有剪掉,而是把它折成如图3形状,试探究∠1+∠2与∠A的关系并说明理由.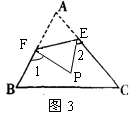
相关知识点
推荐套卷
 4|+|3-cd|的值.
4|+|3-cd|的值.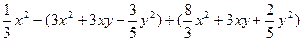 ,其中
,其中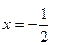 ,y=2
,y=2
 .
.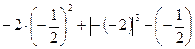 . (2)
. (2)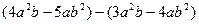
 粤公网安备 44130202000953号
粤公网安备 44130202000953号