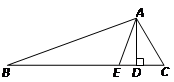如图,已知△ABC中,AD是高,AE是角平分线.
(1)若∠B=20°,∠C=60°,则∠EAD=_______°;
(2)若∠B=a°,∠C=b°(b>a),试通过计算,用a、b的代数式表示∠EAD的度数;
(3)特别地,当△ABC为等腰三角形(即∠B=∠C)时,请用一句话概括此时AD和AE的位置关系:____.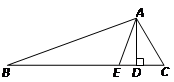
相关知识点
推荐套卷
如图,已知△ABC中,AD是高,AE是角平分线.
(1)若∠B=20°,∠C=60°,则∠EAD=_______°;
(2)若∠B=a°,∠C=b°(b>a),试通过计算,用a、b的代数式表示∠EAD的度数;
(3)特别地,当△ABC为等腰三角形(即∠B=∠C)时,请用一句话概括此时AD和AE的位置关系:____.