如图，在平面直角坐标系中，已知△AOB是等边三角形，点A的坐标是(0，4)，点B在第一象限，点P是x轴上的一个动点，连结AP，并把△AOP绕着点A按逆时针方向旋转，使边A0与AB重合，得到△ABD．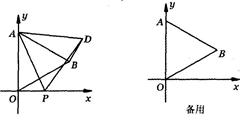
(1)求点B的坐标；
(2)当点P运动到点(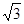
，0)时，求此时点D的坐标；
(3)在点P运动的过程中是否存在某个位置，使△OPD的面积等于
，若存在，请求出符合条件的点P的坐标；若不存在，请说明理由．
；（2）
.
.
的值(1)为正；(2)值为负；(3)值为0.
； (2)
.
，
，
，
，
，π，
.相关知识点
推荐套卷
如图，在平面直角坐标系中，已知△AOB是等边三角形，点A的坐标是(0，4)，点B在第一象限，点P是x轴上的一个动点，连结AP，并把△AOP绕着点A按逆时针方向旋转，使边A0与AB重合，得到△ABD．
(1)求点B的坐标；
(2)当点P运动到点(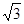，0)时，求此时点D的坐标；
(3)在点P运动的过程中是否存在某个位置，使△OPD的面积等于，若存在，请求出符合条件的点P的坐标；若不存在，请说明理由．
粤公网安备 44130202000953号