两个大小相同且含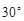
角的三角板ABC和DEC如图①摆放，使直角顶点重合. 将图①中△DEC绕点C逆时针旋转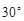得到图②，点F、G分别是CD、DE与AB的交点，点H是DE与AC的交点.
（1）不添加辅助线，写出图②中所有与△BCF全等的三角形；
（2）将图②中的△DEC绕点C逆时针旋转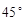
得△D1E1C，点F、G、H的对应点分别为F1、G1、H1，如图③.探究线段D1F1与AH1之间的数量关系，并写出推理过程；
（3）在（2）的条件下，若D1E1与CE交于点I，求证：G1I =CI.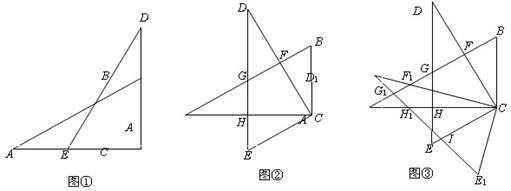
，其中
是上升高度，
是初速度，
是重力加速度（本题中取
），
是抛出后所经过的时间，一物体以
的初速度竖直向上抛出，物体何时在离抛出点25m高的地方?
，其中
，
相关知识点
推荐套卷
粤公网安备 44130202000953号