(本小题满分13分)
平地上有一条水渠,其横断面是一段抛物线弧,如图,已知渠宽为
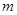 ,渠深为6
,渠深为6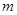 。
。
(1)若渠中水深为4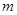 ,求水面的宽,并计算水渠横断面上的过水面积;
,求水面的宽,并计算水渠横断面上的过水面积;
(2)为了增大水渠的过水量,现要把这条水渠改挖(不能填土)成横断面为等腰梯形的水渠,使水渠的底面与地面平行(不改变渠深),要使所挖土的土方量最少,请你设计水渠改挖后的底宽,并求出这个底宽。
相关知识点
推荐套卷
(本小题满分13分)
平地上有一条水渠,其横断面是一段抛物线弧,如图,已知渠宽为
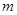 ,渠深为6
,渠深为6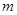 。
。
(1)若渠中水深为4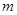 ,求水面的宽,并计算水渠横断面上的过水面积;
,求水面的宽,并计算水渠横断面上的过水面积;
(2)为了增大水渠的过水量,现要把这条水渠改挖(不能填土)成横断面为等腰梯形的水渠,使水渠的底面与地面平行(不改变渠深),要使所挖土的土方量最少,请你设计水渠改挖后的底宽,并求出这个底宽。