在锐角△ABC中，AB=4，BC=5，∠ACB=45°，将△ABC绕点B按逆时针方向旋转，得到△A1BC1．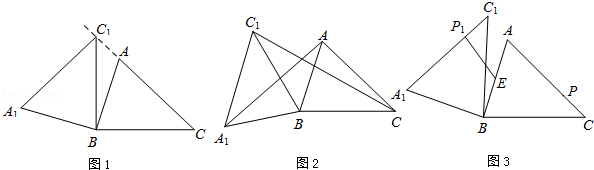
（1）如图1，当点C1在线段CA的延长线上时，求∠CC1A1的度数；
（2）如图2，连接AA1，CC1．若△ABA1的面积为4，求△CBC1的面积；
（3）如图3，点E为线段AB中点，点P是线段AC上的动点，在△ABC绕点B按逆时针方向旋转过程中，点P的对应点是点P1，求线段EP1长度的最大值与最小值．
相关试题
如图所示，直线AB与x轴交于点A，与y轴交于点C（0，2），且与反比例函数
的图象在第二象限内交于点B，过点B作BD⊥x轴于点D，OD=2．
（1）求直线AB的解析式；
（2）若点P是线段BD上一点，且△PBC的面积等于3，求点P的坐标．
．
．
相关知识点
推荐套卷
粤公网安备 44130202000953号