如图,在平面直角坐标系中,二次函数y=ax2+6x+c的图象经过点A(4,0)、B(﹣1,0),与y轴交于点C,点D在线段OC上,OD=t,点E在第二象限,∠ADE=90°,tan∠DAE=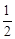 ,EF⊥OD,垂足为F.
,EF⊥OD,垂足为F.
(1)求这个二次函数的解析式;
(2)求线段EF、OF的长(用含t的代数式表示);
(3)当∠ECA=∠OAC时,求t的值.
(图文不相符)
相关知识点
推荐套卷
如图,在平面直角坐标系中,二次函数y=ax2+6x+c的图象经过点A(4,0)、B(﹣1,0),与y轴交于点C,点D在线段OC上,OD=t,点E在第二象限,∠ADE=90°,tan∠DAE=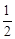 ,EF⊥OD,垂足为F.
,EF⊥OD,垂足为F.
(1)求这个二次函数的解析式;
(2)求线段EF、OF的长(用含t的代数式表示);
(3)当∠ECA=∠OAC时,求t的值.
(图文不相符)