为了了解中小学今年阳光体育运动的开展情况,某市教育局进行了一次随机调查,调查内容是:每天锻炼是否超过1h及锻炼未超过1h的原因.随机调查了720名学生,用所得的数据制成了扇形统计图(图1)和频数分布直方图(图2).
根据图示,请回答以下问题:每天锻炼未超1h的原因中是“没时间”的人数是 ,并补全频数分布直方图;
2012年该市中小学生约32万人,按此调查,可以估计2012年全市中小学生每天锻炼超过1h的约有多少万人?
相关知识点
推荐套卷
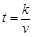 ,其图象为如图所示的一段曲线,且端点为
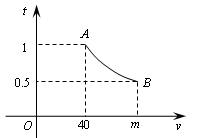
,其图象为如图所示的一段曲线,且端点为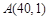 和
和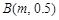 .
.




 粤公网安备 44130202000953号
粤公网安备 44130202000953号