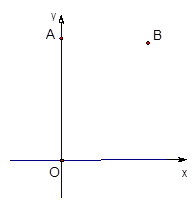
如图，在平面直角坐标系中，点A（0,8），点B（6,8）.
(1)只用直尺（没有刻度）和圆规，求作一个点P，使点P同时满足下列两个条件（要求保留作图痕迹，不必写出作法）
①点p到A，B两点的距离相等；
②点P到∠xoy的两边的距离相等.
(2)直接写出点P的坐标.