在每年召开的市人代会上, 某市财政局都要报告年度市财政预算和执行情况. 以下是根据
2007～2011年度报告中有关数据制作的市财政教育预算与实际投入统计图表的一部分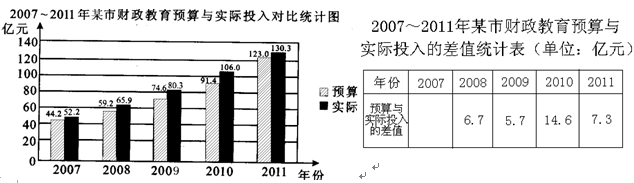
（1）请在表的空格内填入2007年市财政教育实际投入与预算的差值；
（2）求2007～2011年某市财政教育实际投入与预算差值的平均数；
（3）已知2012年某市财政教育预算是141.7亿元, 在此基础上, 如果2012年某市财政教育实际
投入按照(2)中求出的平均数增长, 估计它的金额可能达到多少亿元?
相关试题
．观察下列图形中的棋子：
（1）按照这样的规律摆下去，第4个图形中的棋子个数是多少？
（2）用含
的代数式表示第个图形的棋子个数；
（3）求第20个图形需棋子多少个？
，其中
．
，
是两根柱子在同一灯光下的影子．
，
．
8×；②
－（）
＝8×4；
－（）相关知识点
推荐套卷
粤公网安备 44130202000953号