如图，在
中，点
、
、
分别在
、
、
上，且
，
．
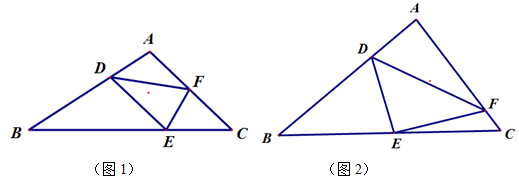
（1）如图1，当
时，图1中是否存在于
相等的线段？若存在，请找出并加以证明．若不存在说明理由．
（2）如图2，当
（其中
）时，若
，
，求
的长（用含
，
的式子表示）．
相关试题
如图，已知☉O的直径AB=8，过A、B两点作☉O的切线AD、BC．
（1）当AD=2，BC=8时，连接OC、OD、CD．
①求△COD的面积．
②试判断直线CD与☉O的位置关系，并说明理由．
（2）若直线CD与☉O相切于点E，设AD=x（x＞0），试用含x的式子表示四边形ABCD的面积S，并探索S是否存在最小值，写出探索过程．
为了节省材料，某水产养殖户利用水库的岸堤（岸堤足够长）为一边，用总长为80m的围网在水库中围成了如图所示的①②③三块矩形区域，而且这三块矩形区域的面积相等．设BC的长度为xm，矩形区域ABCD的面积为ym2．
（1）求y与x之间的函数关系式，并注明自变量x的取值范围；
（2）x为何值时，y有最大值？最大值是多少？
在Rt△ABC中，∠ACB=90°，现将Rt△ABC绕点C逆时针旋转90°，得到Rt△DEC（如图①）
（1）请判断ED与AB的位置关系，并说明理由．
（2）如图②，将Rt△DEC沿CB方向向右平移，且使点D恰好落在AB边上，记平移后的三角形为Rt△DEF，连接AE、DC，求证：∠ACD=∠AED．
已知关于x的方程（x﹣3）（x﹣2）﹣p2=0．
（1）求证：方程总有两个不相等的实数根．
（2）设方程的两根为x1，x2（x1＜x2），则当0≤p
时，请直接写出x1和x2的取值范围．
，设直线AC与抛物线的对称轴交于点P，请求出△ABP的面积．相关知识点
推荐套卷
粤公网安备 44130202000953号