某商店经销一种销售成本为每千克40元的水产品,据市场分析,若按每千克50
元销售,一个月能售出500㎏,销售单价每涨1元,月销售量就减少10㎏,针对这种水产
品,请解答以下问题:
⑴当销售单价定为每千克55元时,计算销售量与月销售利润;
⑵设销售单价为每千克 元,月销售利润为
元,月销售利润为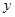 元,求
元,求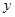 与
与 的关系式;
的关系式;
⑶当销售单价为多少时,月销售利润最大?最大利润是多少?
⑷商店想在销售成本不超过10000元的情况下,使得月销售利润刚好达到8000元,销售单价应为多少?
相关知识点
推荐套卷



 上的概率.
上的概率. 粤公网安备 44130202000953号
粤公网安备 44130202000953号