如图，在四边形ABCD中，AD∥BC，∠C＝90°，BC＝16，DC＝12，AD＝21.动点P从点D出发，沿线段DA的方向以每秒2个单位长的速度运动，动点Q从点C出发，在线段CB上以每秒1个单位长的速度向点B运动，点P，Q分别从点D，C同时出发，当点P运动到点A时，点Q随之停止运动.设运动的时间为t（秒）.
（1）当t=2时，求△BPQ的面积；
(2)若四边形ABQP为平行四边形,求运动时间t.
（3）当t为何值时，以B，P，Q三点为顶点的三角形是等腰三角形？
相关试题
（本题10分）某校为了解2014年八年级学生课外书籍借阅情况，从中随机抽取了40名学生课外书籍借阅情况，将统计结果列出如下的表格，并绘制成如图所示的扇形统计图，其中科普类册数占这40名学生借阅总册数的40%．
| 类别 |
科普类 |
教辅类 |
文艺类 |
其他 |
| 册数（本） |
128 |
80 |
m |
48 |
（1）求表格中字母m的值及扇形统计图中“教辅类”所对应的圆心角a的度数；
（2）该校2014年八年级有500名学生，请你估计该年级学生共借阅教辅类书籍约多少本？
轴两交点的横坐标的平方和为15，求函数解析式及对称轴.已知抛物线y=ax2+bx+c 如图所示，直线x=-1是其对称轴，
（1）确定a，b，c， Δ=b2-4ac的符号，
（2）求证：a-b+c>0，
（3）当x取何值时，y>0；当x取何值时y<0.
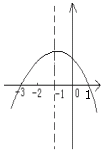
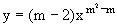+3x+6是二次函数，求m的值，并判断此抛物线开口方向，写出顶点坐标及对称轴.相关知识点
推荐套卷
粤公网安备 44130202000953号