如图,A、B为⊙O上的两个定点,P是⊙O上的动点(P不与A、B重合),我们称∠APB为⊙O上关于A、B的滑动角。
(1)已知∠APB是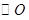 上关于点A、B的滑动角。
上关于点A、B的滑动角。
① 若AB为⊙O的直径,则∠APB=
② 若⊙O半径为1,AB= ,求∠APB的度数
,求∠APB的度数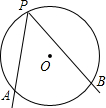
(2)已知 为
为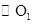 外一点,以
外一点,以 为圆心作一个圆与
为圆心作一个圆与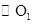 相交于A、B两点,∠APB为
相交于A、B两点,∠APB为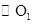 上关于点A、B的滑动角,直线PA、PB分别交
上关于点A、B的滑动角,直线PA、PB分别交 于点M、N(点M与点A、点N与点B均不重合),连接AN,试探索∠APB与∠MAN、∠ANB之间的数量关系。
于点M、N(点M与点A、点N与点B均不重合),连接AN,试探索∠APB与∠MAN、∠ANB之间的数量关系。
相关知识点
推荐套卷
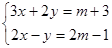 的解互为相反数,求m的值。
的解互为相反数,求m的值。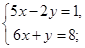 ;(2)
;(2)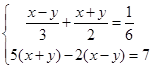
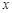 轴上,折叠边AD,使点D落在
轴上,折叠边AD,使点D落在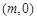 ,其中
,其中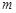 >0.
>0.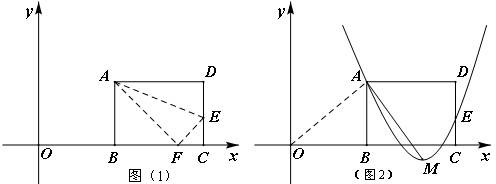
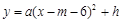 经过图(1)中的A、E两点,如图(2),其顶点为M,连结AM,若∠OAM=90°,求
经过图(1)中的A、E两点,如图(2),其顶点为M,连结AM,若∠OAM=90°,求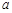 、
、 、
、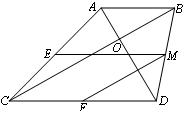
 =_______;
=_______;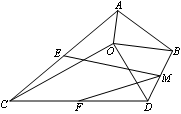
 角(
角( ),其他条件不变,判断
),其他条件不变,判断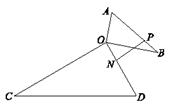
 ,点N在线段OD上,且NO="2." 点P是线段AB上的一个动点,在将△AOB绕点O旋转的过程中,线段PN长度的最小值为_______,最大值为_______.
,点N在线段OD上,且NO="2." 点P是线段AB上的一个动点,在将△AOB绕点O旋转的过程中,线段PN长度的最小值为_______,最大值为_______.
 粤公网安备 44130202000953号
粤公网安备 44130202000953号