小强骑自行车去郊游,如图表示他离家的距离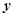 (千米)与所用的时间
(千米)与所用的时间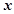 (小时)之间关系的函数图象,小强9点离开家,15点回家.
(小时)之间关系的函数图象,小强9点离开家,15点回家.
根据这个图象,请你回答下列问题:
(1)小强到离家最远的地方需几小时?此时离家多远?
(2)何时开始第一次休息?休息时间多长?
(3)小强返回家时,何时距家21㎞?(写出计算过程).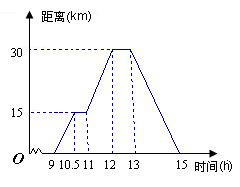
相关知识点
推荐套卷
小强骑自行车去郊游,如图表示他离家的距离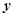 (千米)与所用的时间
(千米)与所用的时间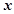 (小时)之间关系的函数图象,小强9点离开家,15点回家.
(小时)之间关系的函数图象,小强9点离开家,15点回家.
根据这个图象,请你回答下列问题:
(1)小强到离家最远的地方需几小时?此时离家多远?
(2)何时开始第一次休息?休息时间多长?
(3)小强返回家时,何时距家21㎞?(写出计算过程).