如图,张大叔从市场上买回一块矩形铁皮,他将此矩形铁皮的四个角各剪去一个边长为1米的正方形后,剩下的部分刚好能围成一个容积为15米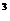 的无盖长方体箱子,且此长方体箱子的底面长比宽多2米,现已知购买这种铁皮每平方米需20元钱,问张大叔购回这张矩形铁皮共花了多少元钱?
的无盖长方体箱子,且此长方体箱子的底面长比宽多2米,现已知购买这种铁皮每平方米需20元钱,问张大叔购回这张矩形铁皮共花了多少元钱?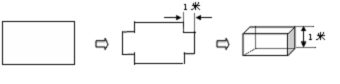
相关知识点
推荐套卷
如图,张大叔从市场上买回一块矩形铁皮,他将此矩形铁皮的四个角各剪去一个边长为1米的正方形后,剩下的部分刚好能围成一个容积为15米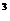 的无盖长方体箱子,且此长方体箱子的底面长比宽多2米,现已知购买这种铁皮每平方米需20元钱,问张大叔购回这张矩形铁皮共花了多少元钱?
的无盖长方体箱子,且此长方体箱子的底面长比宽多2米,现已知购买这种铁皮每平方米需20元钱,问张大叔购回这张矩形铁皮共花了多少元钱?