(10分)设
和
分别是先后抛掷一枚骰子得到的点数，用随机变量
表示方程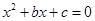
实根的个数（重根按一个计）．
（Ⅰ）求方程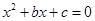有实根的概率；
（Ⅱ）求的分布列和数学期望；
（Ⅲ）求在先后两次出现的点数中有5的条件下，方程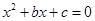有实根的概率.
，B
求点C使
；
，F2
，离心率e=0.8。求此椭圆长轴上
所得的弦长为
。
推荐套卷
(10分)设和分别是先后抛掷一枚骰子得到的点数，用随机变量表示方程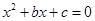实根的个数（重根按一个计）．
（Ⅰ）求方程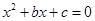有实根的概率；
（Ⅱ）求的分布列和数学期望；
（Ⅲ）求在先后两次出现的点数中有5的条件下，方程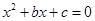有实根的概率.
粤公网安备 44130202000953号