将函数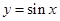
的图象向右平移
个单位, 再将所得图象上各点横坐标伸长到原来的3倍(纵坐标不变), 再将所得图象上各点纵坐标伸长为原来的4倍(横坐标不变), 得到函数
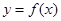的图象；
（Ⅰ）写出函数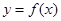的解析式；
（Ⅱ）求此函数的对称中心的坐标；
（Ⅲ）用五点作图法作出这个函数在一个周期内的图象．
相关试题
的最小值为1，
，
．
在
上不是单调函数，求实数
的取值范围．
，集合
．
；
．
的所有棱长都为2，
，平面
⊥平面
，
．
；
的平面角的余弦值；
上是否存在点
，使得
∥平面
，若存在求出
是边长为1的正方形，
⊥平面
⊥平面
；
，且二面角
的大小为
，求
中，
⊥底面
，
，
，
为
的中点，
为
的中点，点
在
上，且
．
⊥平面
；
∥平面
．推荐套卷
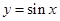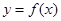将函数的图象向右平移个单位, 再将所得图象上各点横坐标伸长到原来的3倍(纵坐标不变), 再将所得图象上各点纵坐标伸长为原来的4倍(横坐标不变), 得到函数的图象；
（Ⅰ）写出函数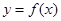的解析式；
（Ⅱ）求此函数的对称中心的坐标；
（Ⅲ）用五点作图法作出这个函数在一个周期内的图象．
粤公网安备 44130202000953号