十一届全国人大常委会第二十次会议审议的个人所得税法修正案草案 (简称"个税法草案"),拟将现行个人所得税的起征点由每月2000元提高到3000元,并将9级超额累进税率修改为7级,两种征税方法的1~5级税率情况见下表:
税级
|
现行征税方法
|
草案征税方法
|
| 月应纳税额
|
税率
|
速算扣除数
|
月应纳税额
|
税率
|
速算扣除数
|
1
|
|
5%
|
0
|
|
5%
|
0
|
2
|
|
10%
|
25
|
|
10%
|
|
3
|
|
15%
|
125
|
|
20%
|
|
4
|
|
20%
|
375
|
|
25%
|
975
|
5
|
|
25%
|
1375
|
|
30%
|
2725
|
注:"月应纳税额"为个人每月收入中超出起征点应该纳税部分的金额.
"速算扣除数"是为快捷简便计算个人所得税而设定的一个数.
例如:按现行个人所得税法的规定,某人今年3月的应纳税额为2600元,他应缴税款可以用下面两种方法之一来计算:
方法一:按1~3级超额累进税率计算,即500×5%+1500×10%十600×15%=265(元).
方法二:用"月应纳税额x适用税率一速算扣除数"计算,即2600×15%一l25=265(元)。
(1)请把表中空缺的"速算扣除数"填写完整;
(2)甲今年3月缴了个人所得税1060元,若按"个税法草案"计算,则他应缴税款多少元?
(3)乙今年3月缴了个人所得税3千多元,若按"个税法草案"计算,他应缴的税款恰好不变,那么乙今年3月所缴税款的具体数额为多少元?

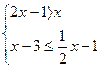
 交于M(x1,y1)
交于M(x1,y1)
 (万元).当地政府
(万元).当地政府 (万元)
(万元) 粤公网安备 44130202000953号
粤公网安备 44130202000953号