函数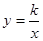
和
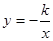
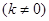的图象关于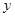
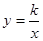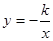
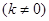轴对称，我们把函数和叫做互为“镜子”函数．类似地，如果函数
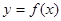和
的图象关于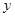轴对称，那么我们就把函数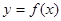和叫做互为“镜子”函数．
（1）请写出函数y=2x－3的“镜子”函数： ▲ ;
（2）函数 ▲ 的“镜子”函数是y=－x2+2x+3；
（3）如图，一条直线与一对“镜子”函数
（
＞
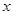）和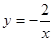
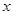（＜）的图象分别交于点A，B，C，如果
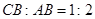，点
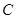在函数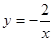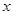（＜）的“镜子”函数上的对应点的横坐标是1/2，求点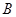
的坐标． 
（4）
”连接起来。
，
， 
， 
， 
，5，
，
，
，
，0，
，
，
，
在数轴上的对应点的位置填空。
0（2）
0 
0（4）
0
，
，
，
，
，
，……，观察规律，试猜想
的个位数是。相关知识点
推荐套卷
粤公网安备 44130202000953号