如图1,在正方形 中,对角线
中,对角线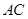 与
与 相交于点
相交于点 ,
, 平分
平分 ,交
,交 于点
于点 .
.
(1)求证: ;
;
(2)点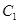 从点
从点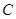 出发,沿着线段
出发,沿着线段 向点
向点 运动(不与点
运动(不与点 重合),同时点
重合),同时点 从点
从点 出发,沿着
出发,沿着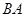 的延长线运动,点
的延长线运动,点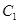 与
与 的运动速度相同,当动点
的运动速度相同,当动点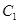 停止运动时,另一动点
停止运动时,另一动点 也随之停止运动.如图2,
也随之停止运动.如图2, 平分
平分 ,交
,交 于点
于点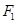 ,过点
,过点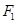 作
作 ,垂足为
,垂足为 ,请猜想
,请猜想 ,
, 与
与 三者之间的数量关系,并证明你的猜想;
三者之间的数量关系,并证明你的猜想;
(3)在(2)的条件下,当 ,
,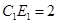 时,求
时,求 的长
的长
相关知识点
推荐套卷
如图1,在正方形 中,对角线
中,对角线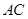 与
与 相交于点
相交于点 ,
, 平分
平分 ,交
,交 于点
于点 .
.
(1)求证: ;
;
(2)点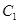 从点
从点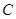 出发,沿着线段
出发,沿着线段 向点
向点 运动(不与点
运动(不与点 重合),同时点
重合),同时点 从点
从点 出发,沿着
出发,沿着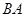 的延长线运动,点
的延长线运动,点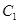 与
与 的运动速度相同,当动点
的运动速度相同,当动点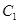 停止运动时,另一动点
停止运动时,另一动点 也随之停止运动.如图2,
也随之停止运动.如图2, 平分
平分 ,交
,交 于点
于点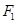 ,过点
,过点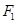 作
作 ,垂足为
,垂足为 ,请猜想
,请猜想 ,
, 与
与 三者之间的数量关系,并证明你的猜想;
三者之间的数量关系,并证明你的猜想;
(3)在(2)的条件下,当 ,
,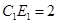 时,求
时,求 的长
的长