(本小题满分9分)
如图一次函数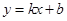 (
( )的图象分别交
)的图象分别交 轴、
轴、 轴于点
轴于点 ,与反比例函数
,与反比例函数 图象在第二象限交于点
图象在第二象限交于点 ,
,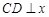 轴于点
轴于点 ,OA=OD.
,OA=OD.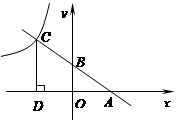
⑴求m的值和一次函数的表达式;
⑵在 轴上求点
轴上求点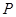 ,使△CAP为等腰三角形(求出所有符合条件的点).
,使△CAP为等腰三角形(求出所有符合条件的点).
相关知识点
推荐套卷
(本小题满分9分)
如图一次函数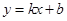 (
( )的图象分别交
)的图象分别交 轴、
轴、 轴于点
轴于点 ,与反比例函数
,与反比例函数 图象在第二象限交于点
图象在第二象限交于点 ,
,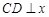 轴于点
轴于点 ,OA=OD.
,OA=OD.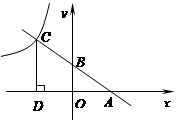
⑴求m的值和一次函数的表达式;
⑵在 轴上求点
轴上求点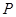 ,使△CAP为等腰三角形(求出所有符合条件的点).
,使△CAP为等腰三角形(求出所有符合条件的点).