某件商品的成本价为15元,据市场调查得知,每天的销量y(件)与价格x(元)有下列关系:
| 销售价格x |
20 |
25 |
30 |
50 |
| 销售量y |
15 |
12 |
10 |
6 |
(1)根据表中数据,在直角坐标系中描出实数对(x,y)的对应点,并画出图象。
(2)猜测确定y与x间的关系式。
(3)设总利润为W元,试求出W与x之间的函数关系式,若售价不超过30元,求出当日的销售单价定为多少时,才能获得最大利润?
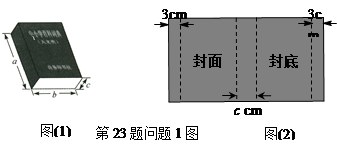
相关知识点
推荐套卷
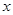 ,求S与
,求S与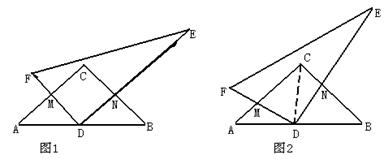
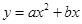 经过A、D两点,如图所示.
经过A、D两点,如图所示.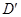 的坐标及a、b的值;
的坐标及a、b的值;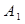 ,点D的对应点为
,点D的对应点为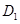 ,当抛物线平移到某个位置时,恰好使得点O是y轴上到
,当抛物线平移到某个位置时,恰好使得点O是y轴上到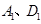 两点距离之和
两点距离之和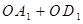 最短的一点,求此抛物线的解析式.
最短的一点,求此抛物线的解析式.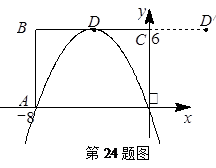

 粤公网安备 44130202000953号
粤公网安备 44130202000953号