在所给的网格图(每小格边长均为1的正方形)中,完成下列各题:
(1)将△ABC向右平移4个单位得到△A1B1C1;
(2)以直线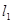 为对称轴作△ABC的轴对称图形△
为对称轴作△ABC的轴对称图形△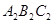 ;
;
(3)△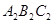 可以看作是由△A1B1C1先向左平移4个单位,再以直线
可以看作是由△A1B1C1先向左平移4个单位,再以直线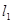 为对称轴作轴对
为对称轴作轴对
称变换得到的。除此以外,△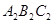 还可以看作是由△A1B1C1经怎样变换得到的?请选择一种方法,写出图形变换的步骤。
还可以看作是由△A1B1C1经怎样变换得到的?请选择一种方法,写出图形变换的步骤。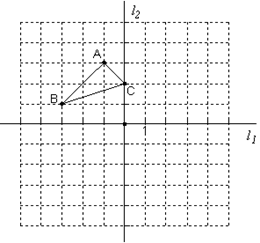
相关知识点
推荐套卷
在所给的网格图(每小格边长均为1的正方形)中,完成下列各题:
(1)将△ABC向右平移4个单位得到△A1B1C1;
(2)以直线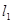 为对称轴作△ABC的轴对称图形△
为对称轴作△ABC的轴对称图形△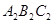 ;
;
(3)△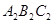 可以看作是由△A1B1C1先向左平移4个单位,再以直线
可以看作是由△A1B1C1先向左平移4个单位,再以直线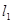 为对称轴作轴对
为对称轴作轴对
称变换得到的。除此以外,△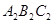 还可以看作是由△A1B1C1经怎样变换得到的?请选择一种方法,写出图形变换的步骤。
还可以看作是由△A1B1C1经怎样变换得到的?请选择一种方法,写出图形变换的步骤。
