如图，在平面直角坐标系中，点C的坐标为（0，4），动点A以每秒1个单位长的速度，从点O出发沿
轴的正方向运动，M是线段AC的中点．将线段AM以点A为中心，沿顺时针方向旋转
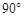，得到线段AB．过点B作轴的垂线，垂足为E，过点C作
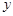轴的垂线，交直线BE于点D．运动时间为
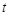秒．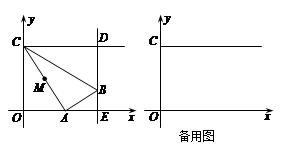
（1）当点B与点D重合时，求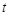的值；
（2）设△BCD的面积为S，当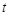为何值时，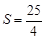
?
（3）连接MB，当MB∥OA时，如果抛物线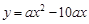
的顶点在△ABM内部（不包括边），求a的取值范围．
相关试题
，∠C=∠D.求证：CB=DB.
如图，OA、OB表示两条相交的公路，点M、N是两个工厂，现在要在∠AOB内建立一个货物中转站，使中转站到公路OA、OB的距离相等，并且到工厂M、N的距离也相等，用尺规作出货物中转站的位置.
相关知识点
推荐套卷
粤公网安备 44130202000953号