如图，在四边形ABCD中，对角线AC、BD相交于点O，直线MN经过点O，设锐角∠DOC=∠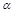
，将△DOC以直线MN为对称轴翻折得到△D’OC’，直线A D’、B C’相交于点P．
（Ⅰ）当四边形ABCD是矩形时，如图1，请猜想A D’、B C’的数量关系以及∠APB与∠α的大小关系；
（Ⅱ）当四边形ABCD是平行四边形时，如图2，（1）中的结论还成立吗？
（Ⅲ）当四边形ABCD是等腰梯形时，如图3，∠APB与∠α有怎样的数量关系？请证明．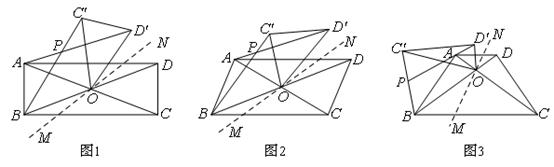
相关试题
于点M，CF⊥AB于点F交BD于点E，
,
的方程
有两个不相等的实数根，
的取值范围.②当k为最小整数时求原方程的解。
的坐标；
相关知识点
推荐套卷
粤公网安备 44130202000953号