如图,在梯形ABCD中,AD∥BC,E是BC上的一点,且CE=8,BC=12,CD=4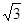 ,∠C=30°,∠B=60°。点P是线段BC边上一动点(包括B、C两点),设PB的长是x。
,∠C=30°,∠B=60°。点P是线段BC边上一动点(包括B、C两点),设PB的长是x。
(1)当x为何值时,以点P、A、D、E为顶点的四边形为直角梯形。
(2)当x为何值时,以点P、A、D、E为顶点的四边形为平行四边形。
(3)P在BC 上运动时,以点P、A、D、E为顶点的四边形能否为菱形。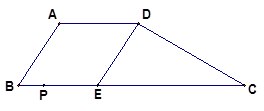
相关知识点
推荐套卷
如图,在梯形ABCD中,AD∥BC,E是BC上的一点,且CE=8,BC=12,CD=4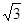 ,∠C=30°,∠B=60°。点P是线段BC边上一动点(包括B、C两点),设PB的长是x。
,∠C=30°,∠B=60°。点P是线段BC边上一动点(包括B、C两点),设PB的长是x。
(1)当x为何值时,以点P、A、D、E为顶点的四边形为直角梯形。
(2)当x为何值时,以点P、A、D、E为顶点的四边形为平行四边形。
(3)P在BC 上运动时,以点P、A、D、E为顶点的四边形能否为菱形。