(本小题满分7分)有3张形状材质相同的不透明卡片,正面分别写有1、2、-3,三个数字.将这三张卡片背面朝上洗匀后,第一次从中随机抽取一张,并把这张卡片标有的数字作为一次函数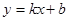 中
中 的值;第二次从余下的两张卡片中再随机抽取一张,上面标有的数字作为
的值;第二次从余下的两张卡片中再随机抽取一张,上面标有的数字作为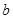 的值.
的值.
(1) 的值为正数的概率是 ;
的值为正数的概率是 ;
(2)用画树状图或列表法求所得到的一次函数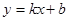 的图像经过第一、三、四象限的概率.
的图像经过第一、三、四象限的概率.
相关知识点
推荐套卷
(本小题满分7分)有3张形状材质相同的不透明卡片,正面分别写有1、2、-3,三个数字.将这三张卡片背面朝上洗匀后,第一次从中随机抽取一张,并把这张卡片标有的数字作为一次函数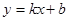 中
中 的值;第二次从余下的两张卡片中再随机抽取一张,上面标有的数字作为
的值;第二次从余下的两张卡片中再随机抽取一张,上面标有的数字作为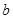 的值.
的值.
(1) 的值为正数的概率是 ;
的值为正数的概率是 ;
(2)用画树状图或列表法求所得到的一次函数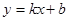 的图像经过第一、三、四象限的概率.
的图像经过第一、三、四象限的概率.