(1)如图,试用直尺与圆规在平面内确定一点O,使得点O到Rt△ABC的两边AC、BC的距离相等,并且点O到A、B两点的距离也相等.(不写作法,但需保留作图痕迹)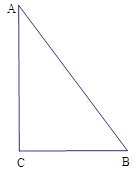
(2)在(1)中,作OM⊥AC于M, ON⊥BC于N,连结A0、BO.求证:△OMA≌△ONB.
相关知识点
推荐套卷
(1)如图,试用直尺与圆规在平面内确定一点O,使得点O到Rt△ABC的两边AC、BC的距离相等,并且点O到A、B两点的距离也相等.(不写作法,但需保留作图痕迹)
(2)在(1)中,作OM⊥AC于M, ON⊥BC于N,连结A0、BO.求证:△OMA≌△ONB.