直三棱柱ABC－A1B1C1中， AC=BC=AA1=2，∠ACB=90°.E为BB1的中点，D点在AB上且DE=
.
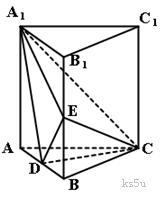
（Ⅰ）求证：CD⊥平面A1ABB1；
（Ⅱ）求三棱锥A1－CDE的体积.
相关试题
的前n项和为
，且
，
. 
；（2）设
，求数列
的前n项和
.
的离心率
，连接椭圆的四个顶点得到的菱形的面积为4.
与椭圆相交于不同的两点A,B。已知点A的坐标为
。若
，求直线
，求曲线过点
的切线方程。
其中
.
.
相关知识点
推荐套卷
直三棱柱ABC－A1B1C1中， AC=BC=AA1=2，∠ACB=90°.E为BB1的中点，D点在AB上且DE=.
（Ⅰ）求证：CD⊥平面A1ABB1；
（Ⅱ）求三棱锥A1－CDE的体积.
粤公网安备 44130202000953号