(本小题满分12分)
某班主任统计本班50名学生放学回家后学习时间的数据,用条形图表示(如图)。
(1)求该班学生每天在家学习时间的平均值;
(2)该班主任用分层抽样方法(按学习时间分五层)选出10个学生谈话,求在学习时间为1个小时的学生中选出的人数;
(3)假设学生每天在家学习时间为18时至23时,已知甲每天连续学习2小时,乙每天连续学习3小时,求19时至20时甲、乙都在学习的概率.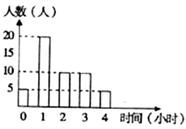
推荐套卷
(本小题满分12分)
某班主任统计本班50名学生放学回家后学习时间的数据,用条形图表示(如图)。
(1)求该班学生每天在家学习时间的平均值;
(2)该班主任用分层抽样方法(按学习时间分五层)选出10个学生谈话,求在学习时间为1个小时的学生中选出的人数;
(3)假设学生每天在家学习时间为18时至23时,已知甲每天连续学习2小时,乙每天连续学习3小时,求19时至20时甲、乙都在学习的概率.