某商场试销一种成本为每件60元的服装,规定试销期间销售单价不低于成本单价,且获利不得高于45%,经试销发现,销售量 (件)与销售单价
(件)与销售单价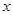 (元)符合一次函数
(元)符合一次函数 ,且
,且 时,
时, ;
;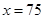 时,
时,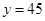 .
.
(1)求一次函数 的表达式;
的表达式;
(2)若该商场获得利润为 元,试写出利润
元,试写出利润 与销售单价
与销售单价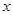 之间的关系式;销售单价定为多少元时,商场可获得最大利润,最大利润是多少元?
之间的关系式;销售单价定为多少元时,商场可获得最大利润,最大利润是多少元?
(3)若该商场获得利润不低于500元,试确定销售单价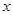 的范围.
的范围.
相关知识点
推荐套卷
某商场试销一种成本为每件60元的服装,规定试销期间销售单价不低于成本单价,且获利不得高于45%,经试销发现,销售量 (件)与销售单价
(件)与销售单价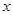 (元)符合一次函数
(元)符合一次函数 ,且
,且 时,
时, ;
;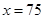 时,
时,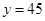 .
.
(1)求一次函数 的表达式;
的表达式;
(2)若该商场获得利润为 元,试写出利润
元,试写出利润 与销售单价
与销售单价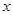 之间的关系式;销售单价定为多少元时,商场可获得最大利润,最大利润是多少元?
之间的关系式;销售单价定为多少元时,商场可获得最大利润,最大利润是多少元?
(3)若该商场获得利润不低于500元,试确定销售单价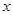 的范围.
的范围.