已知
是公差为d的等差数列，
是公比为q的等比数列
（Ⅰ）若 
，是否存在
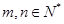，有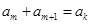
？请说明理由；
（Ⅱ）若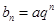
（a、q为常数，且aq
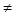0）对任意m存在k，有
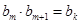，试求a、q满足的充要条件；
（Ⅲ）若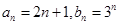
试确定所有的p,使数列中存在某个连续p项的和式数列中的一项，请证明.
中,若
，且
为锐角，求角
.
.
，
，求证：
.
的值.
.
的最小正周期;
上的最大值和最小值.
，
都是锐角，
，
，求
的值.
，
，求
的值.推荐套卷
已知是公差为d的等差数列，是公比为q的等比数列
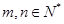（Ⅰ）若 ，是否存在，有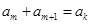？请说明理由；
（Ⅱ）若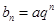（a、q为常数，且aq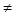0）对任意m存在k，有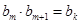，试求a、q满足的充要条件；
（Ⅲ）若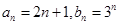试确定所有的p,使数列中存在某个连续p项的和式数列中的一项，请证明.
粤公网安备 44130202000953号