高三年级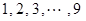
班参加高考体检，
个班中，任选
个班先参加视力检查． （I）求这个班中恰有
个班班级序号是偶数的概率；
(II)设
为这个班中两班序号相邻的组数（例如：若选出的班为
班，则有两组相邻的，
班和
班，此时的值是
）．求随机变量的分布列及其数学期望
．
相关试题
，
，
．
ABC的面积．
（
）的最小值正周期是
．
的值；
的最大值，并且求使
的集合．
时，
的最小值为– 2 ，求a的值．
．
的值；
的单调递增区间．
．求
的值．相关知识点
推荐套卷
高三年级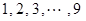班参加高考体检，个班中，任选个班先参加视力检查． （I）求这个班中恰有个班班级序号是偶数的概率；
(II)设为这个班中两班序号相邻的组数（例如：若选出的班为班，则有两组相邻的，班和班，此时的值是）．求随机变量的分布列及其数学期望．
粤公网安备 44130202000953号