有四张形状、大小和质地相同的卡片A、B、C、D,正面分别写有一个正多边形(所有正多边形的边长相等),把四张卡片洗匀后正面朝下放在桌面上,从中随机抽取一张(不放回),接着再随机抽取一张.
请你用画树形图或列表的方法列举出可能出现的所有结果;
如果在(1)中各种结果被选中的可能性相同,求两次抽取的正多边形能构成平面镶嵌的概率;
若两种正多边形构成平面镶嵌,p、q表示这两种正多边形的个数,x、y表示对应正多边形的每个内角的度数,则有方程px+qy=360,求每种平面镶嵌中p、q的值.
相关知识点
推荐套卷
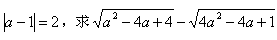 的值
的值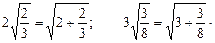
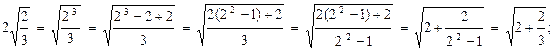
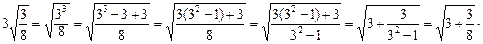
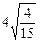 的结果,并写出验证过程;
的结果,并写出验证过程;




 粤公网安备 44130202000953号
粤公网安备 44130202000953号