(本小题满分14分) 设函数
.
（Ⅰ）当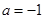
时，求函数
的单调区间和极大值点；
（Ⅱ）已知
，若函数的图象总在直线
的下方，求
的取值范围；
（Ⅲ）记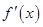
为函数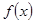
的导函数．若
，试问：在区间
上是否存在
（
）个正数
…
，使得
成立？请证明你的结论.
，且
的最大值。
，比较
与
的大小。
，求证：
，且
，求证：
推荐套卷
(本小题满分14分) 设函数.
（Ⅰ）当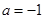时，求函数的单调区间和极大值点；
（Ⅱ）已知，若函数的图象总在直线的下方，求的取值范围；
（Ⅲ）记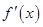为函数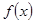的导函数．若，试问：在区间上是否存在（）个正数…，使得成立？请证明你的结论.
粤公网安备 44130202000953号