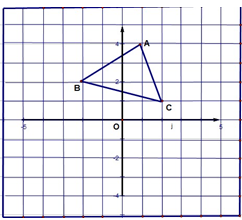
如图,在平面直角坐标系中,点O是坐标原点,四边形AOCB是梯形,AB∥OC,点A的坐标为(0,8),点C的坐标为(10,0),OB=OC.点P从C点出发,沿线段CO以5个单位/秒的速度向终点O匀速运动,过点P作PH⊥OB,垂足为H.
(1)求点B的坐标;
(2)设△HBP的面积为S(S≠0),点P的运动时间为t秒,求S与t之间的函数关系式;当t为何值时,△HBP的面积最大,并求出最大面积;
(3)分别以P、H为圆心,PC、HB为半径作⊙P和⊙H,当两圆外切时,求此时t的值.
相关知识点
推荐套卷
 .
.
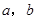 的值;
的值; 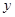 轴上是否存在点C,使得△ABC的面积是12?若存在,求出点C的坐标;若不存在,请说明理由;
轴上是否存在点C,使得△ABC的面积是12?若存在,求出点C的坐标;若不存在,请说明理由; 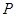 是
是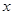 轴的距离为3,若点
轴的距离为3,若点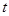 为多少秒时,四边形ABPQ的面积S为15个平方单位?写出此时Q点的坐标.
为多少秒时,四边形ABPQ的面积S为15个平方单位?写出此时Q点的坐标.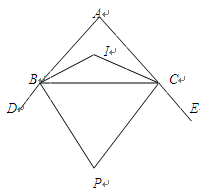
 ,∠C=
,∠C= ,AE是△ABC的角平分线,AD是BC上的高.求∠EAD的度数.
,AE是△ABC的角平分线,AD是BC上的高.求∠EAD的度数.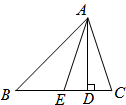
 粤公网安备 44130202000953号
粤公网安备 44130202000953号