小明同学看到路边上有人设摊玩“有奖掷币”游戏，规则是：交2元钱可以玩一次掷硬币游戏，每次同时掷两枚硬币，如果出现两枚硬币正面朝上，奖金5元；如果是其它情况，则没有奖金（每枚硬币落地只有正面朝上和反面朝上两种情况）．小明拿不定主意究竟是玩还是不玩，请同学们帮帮忙！
（1）请用列表或画树形图的方法求出中奖的概率；
（2） 如果有100人，每人玩一次这种游戏，大约有 人中奖，奖金共约是 元；设摊者约获利 元；
（3） 通过以上“有奖”游戏，你从中可得到什么启示？
相关试题
请你在纸上画一个等腰三角形ABC（如图），使得
．
（1）请你判断一下
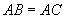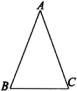
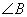与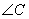
有什么大小关系呢？你的依据是什么？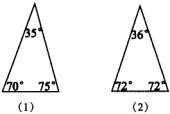
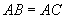（2）请你再深入地思考一个问题：若只知道与相等，请你判断一下这个三角形是什么形状的呢？并说明你的探索思路．
（3）由第（2）你会得到一个什么结论呢？请用一句话概括出来．
（4）现在给出两个三角形（如图），请你把图（1）分割成两个等腰三角形，把图（2）分割成三个等腰三角形．动动脑筋呀！
，小明过点A和BC边的中点D又架了一个细木条，经测量
，你在不用任何测量工具的前提下，能得到
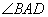和
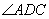的度数吗？
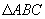中，DE垂直平分AC，交C于点E，交BC于点D，
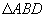的周长是20厘米，AC长为8厘米，你能判断出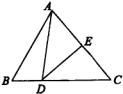
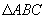老师正叙述这样一道题：请同学们画出一个
，然后画出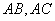
的中垂线，且交于点P．请同学们想一下点P到三角形三个顶点
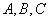的距离如何？小明马上就说：“相等．”他是随便说的吗？你同意他的说法吗？请说明你的理由．
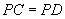，并且使点P到
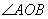的两边的距离相等，并说明你的理由．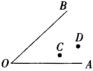
相关知识点
推荐套卷
粤公网安备 44130202000953号