（本题6分）如图，在方格纸中，△ABC的三个顶点及D，E，F，G，H五个点都在小方格的顶点上．现以点D，E，F，G，H中的三个点为顶点画三角形．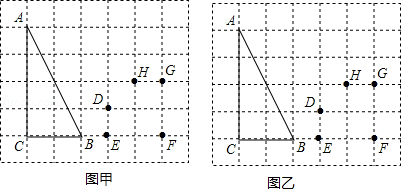
（1）在图甲中画出一个三角形与△ABC相似且相似比为1：2．
（2）在图乙中画出一个三角形与△ABC的面积比为1：4但不相似．
Φ
．
Φ
，请仿照例题计算：
Φ
Φ
Φ
的值，其中
，
．
相关知识点
推荐套卷
（本题6分）如图，在方格纸中，△ABC的三个顶点及D，E，F，G，H五个点都在小方格的顶点上．现以点D，E，F，G，H中的三个点为顶点画三角形．
（1）在图甲中画出一个三角形与△ABC相似且相似比为1：2．
（2）在图乙中画出一个三角形与△ABC的面积比为1：4但不相似．
粤公网安备 44130202000953号