如图,直线l经过点A(1,0),且与曲线 (x>0)交于点B(2,1).过点P(p,p-1)(p≥2)作x轴的平行线分别交曲线
(x>0)交于点B(2,1).过点P(p,p-1)(p≥2)作x轴的平行线分别交曲线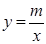 (x>0)和
(x>0)和 (x<0)于M,N两点.
(x<0)于M,N两点.
求m的值及直线l的解析式;
是否存在实数p,使得S△AMN=4S△APM?若存在,请求出所有满足条件的p的值;若不存在,请说明理由
相关知识点
推荐套卷
如图,直线l经过点A(1,0),且与曲线 (x>0)交于点B(2,1).过点P(p,p-1)(p≥2)作x轴的平行线分别交曲线
(x>0)交于点B(2,1).过点P(p,p-1)(p≥2)作x轴的平行线分别交曲线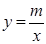 (x>0)和
(x>0)和 (x<0)于M,N两点.
(x<0)于M,N两点.
求m的值及直线l的解析式;
是否存在实数p,使得S△AMN=4S△APM?若存在,请求出所有满足条件的p的值;若不存在,请说明理由