（本小题满分l2分）已知数列{an}中，a1＝1，a2＝3且2an＋1＝an＋2＋an（n∈N*）．数列{bn}的前n项和为Sn，其中b1＝－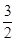
，bn＋1＝－
Sn（n∈N*）．
（1）求数列{an}和{bn}的通项公式；
（2）若Tn＝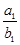
＋
＋…＋
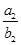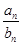，求Tn的表达式
相关试题
中，
，且前
项的算术平均数等于第
倍
．
项；
（m为常数，且m>0）有极大值9.
的切线，求此直线方程
、
、
，
，求证
，求实数
使
成立.（其中
为
的共轭复数）
,它们各自的最小值恰好是函数
的三个零点（其中t是常数，且0<t<1）
，若
，求f(x)推荐套卷
（本小题满分l2分）已知数列{an}中，a1＝1，a2＝3且2an＋1＝an＋2＋an（n∈N*）．数列{bn}的前n项和为Sn，其中b1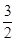＝－，bn＋1＝－Sn（n∈N*）．
（1）求数列{an}和{bn}的通项公式；
（2）若Tn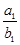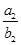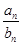＝＋＋…＋，求Tn的表达式
粤公网安备 44130202000953号