(本小题满分13分)等差数列{an}中,公差d≠0,已知数列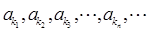 是等比数列,其中k1=1,k2=7,k3=25.
是等比数列,其中k1=1,k2=7,k3=25.
(1)求数列{kn}的通项;
(2)若a1=9,设bn= 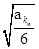 +
+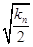 ,Sn=b12+b22+b32+…+ bn2, Tn=
,Sn=b12+b22+b32+…+ bn2, Tn= 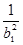 +
+ +
+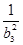 +…+
+…+ ,试判断数列{Sn+Tn}前100项中有多少项是能被4整除的整数。
,试判断数列{Sn+Tn}前100项中有多少项是能被4整除的整数。
推荐套卷
(本小题满分13分)等差数列{an}中,公差d≠0,已知数列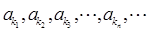 是等比数列,其中k1=1,k2=7,k3=25.
是等比数列,其中k1=1,k2=7,k3=25.
(1)求数列{kn}的通项;
(2)若a1=9,设bn= 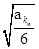 +
+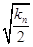 ,Sn=b12+b22+b32+…+ bn2, Tn=
,Sn=b12+b22+b32+…+ bn2, Tn= 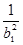 +
+ +
+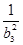 +…+
+…+ ,试判断数列{Sn+Tn}前100项中有多少项是能被4整除的整数。
,试判断数列{Sn+Tn}前100项中有多少项是能被4整除的整数。