如图，在平面直角坐标系中，将一块腰长为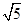
的等腰直角三角板ABC放在第二象限，且斜靠在两坐标轴上，直角顶点C的坐标为（
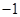，0），点B在抛物线
上．
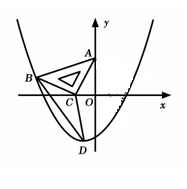
（1）点A的坐标为 ，点B的坐标为 ；
（2）抛物线的解析式为 ；
（3）设（2）中抛物线的顶点为D，求△DBC的面积；
（4）在抛物线上是否还存在点P（点B除外），使ΔACP仍然是以AC为直角边的等腰直角三角形？若存在，请直接写出所有点P的坐标；若不存在，请说明理由。
已知抛物线
(a≠0)的顶点在直线
上，且过点A(4，0)．
⑴求这个抛物线的解析式；
⑵设抛物线的顶点为P，是否在抛物线上存在一点B，使四边形OPAB为梯形？若存在，求出点B的坐标；若不存在，请说明理由.
⑶设点C(1，－3)，请在抛物线的对称轴确定一点D，使
的值最大，请直接写出点D的坐标.
在平面直角坐标系中，四边形OBCD是正方形，且D（0，2），点E是线段OB延长线上一点，M是线段OB上一动点（不包括点O、B），作MN⊥DM，垂足为M，交∠CBE的平分线于点N .写出点C的坐标；
求证：MD = MN；
连接DN交BC于点F，连接FM，下列两个结论：①FM的长度不变；②MN平分∠FMB，其中只有一个结论是正确的，请你指出正确的结论，并给出证明.
若正整数a、b、c满足方程a2+b2=c2 ,则称这一组正整数（a、b、c）为“商高数”，下面列举五组“商高数”：（3，4，5），（5，12，13），（6，8，10），（7，24，25），（12，16，20），注意这五组“商高数”的结构有如下规律：
根据以上规律，回答以下问题：商高数的三个数中，有几个偶数，几个奇数？
写出各数都大于30的两组商高数。
用两个正整数m、n（m＞n）表示一组商高数，并证明你的结论。
已知关于x的一元二次方程x2＋4x＋m－1＝0。请你为m选取一个合适的整数，使得到的方程有两个不相等的实数根；
设α、β是(1)中你所得到的方程的两个实数根，求α2＋β2＋αβ的值。
,
,
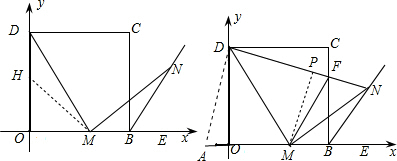
的有理化因式是 . 
分母有理化得 .
="_________;(2)" 
="________;(3)" 
=______.．
.
粤公网安备 44130202000953号